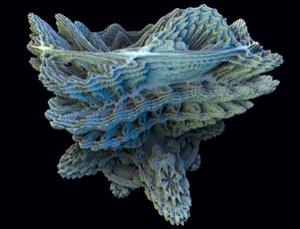
 Migliorano le simulazioni tridimensionali dei frattali di Mandelbrot
Migliorano le simulazioni tridimensionali dei frattali di Mandelbrot
CRONACA – Sembra quasi di poterlo toccare con mano: a oggi “Mandelbulb” secondo i suoi inventori è la migliore – anche se non ancora perfetta – rappresentazione tridimensionale che sia stata fatta della più famosa equazione frattale, l’insieme di Mandelbrot. Un frattale è un oggetto geometrico che ripete all’infinito la sua struttura, che cioè si può osservare a qualsiasi scala senza cambiare d’aspetto, caratteristica nota col nome di autosomiglianza.
I frattali vengono descritti da equazioni piuttosto semplici scritte con i numeri complessi. Le bellissime immagini che siamo abituati a vedere sono create ripetendo per un grande numero di volte una semplice procedura: l’equazione viene risolta per un dato numero, il risultato viene poi usato come incognita per risolvere la stessa equazione e così via. Tutti i risultati vengono tradotti poi in punti in un’immagine.
L’equazione frattale più famosa è l’insieme di Mandelbrot 2D ma ne esistono di altre a due e tre dimensioni. Già in precedenza qualcuno ha cercato di rappresentare un insieme di Mandelbrot 3D, ma secondo Daniel White, un creatore di immagini frattali di Bedford nel Regno Unito, questi tentativi non mostrano realmente il comportamento di frattali. Tutte le tecniche utilizzate fino ad ora mancano infatti di mostrarne la caratteristica principale, l’autosomiglianza.
White ha osservato il problema da un punto di vista geometrico. Normalmente questo approccio sfrutta le proprietà dei numeri complessi: le operazioni su questi numeri corrispondo a rotazioni e traslazioni nel “piano complesso” (che descrive questi numeri) che possono essere tradotte in un’immagine, dove i colori invece rappresentano il numero di iterazioni, cioè quante volte l’equazione viene ricalcolata sulla base dei risultati precedenti.
White ha provato a fare queste rotazioni e traslazioni in un piano tridimensionale, senza usare però i numeri complessi, perché questi possono essere descritti solo in un piano bidimensionale. White ha messo a punto una nuova formula che è stata integrata da un collega di White, Paul Nylander. I due stanno ancora migliorando la metodologia, ma il risultato ottenuto sinora è a detta di White il più vicino mai ottenuto alle equazioni di Mandelbrot.





