Il ruolo della geometria non commutativa nella fisica teorica

RICERCANDO ALL’ESTERO – “La matematica è un linguaggio in cui formulare i problemi. Permette di analizzare i sistemi, le loro operazioni e le loro strutture, alla ricerca di schemi che si ripetono, l’uguale nel diverso come diceva Platone. È molto produttivo quando un matematico può dare un contributo a problemi fisici; trovo affascinante che ci sia questo magico interscambio tra le due discipline”.

Nome: Francesca Arici
Età: 30 anni
Nata a: Brescia
Vivo a: Nijmegen (Paesi Bassi)
Dottorato in: Matematica fisica (Trieste)
Ricerca: Quantizzazione e riduzione delle teorie di gauge su reticolo
Istituto: Institute for Mathematics, Astrophysics and Particle Physics (Nijmegen, Paesi Bassi)
Interessi: suono il violoncello e la chitarra, mi piace andare a teatro e al cinema, studiare le lingue, leggere
Di Nijmegen mi piace: il fiume, il centro storico
Di Nijmegen non mi piace: il sistema sanitario olandese, i negozi chiudono alle 17
Pensiero: Just because some of us can read and write and do a little math, that doesn’t mean we deserve to conquer the Universe (Kurt Vonnegut)

Esistono diversi problemi di fisica teorica che possono essere formulati in modo rigoroso grazie alla matematica. Ne sono un esempio le teorie di campo, un tipo di teorie di gauge, che presentano ancora diverse questioni aperte e per le quali la matematica può dare una mano a trovare la soluzione.

Di cosa parlano le teorie di gauge?
Il termine gauge significa letteralmente scartamento ferroviario, in riferimento alla distanza tra le rotaie in un binario. Sono teorie usate nella fisica delle particelle basate sullo studio delle simmetrie di un sistema, dove per simmetrie intendo trasformazioni che lasciano il sistema invariato. Lo studio delle simmetrie ci aiuta a comprendere la fisica di un certo sistema grazie al fatto che dal teorema di Noether sappiamo che a ogni simmetria corrisponde una quantità conservata (come l’energia, la velocità di rotazione, il momento di una particella).

Un esempio di teoria di gauge è l’elettrostatica: in ogni punto dello spazio di un campo elettrico è possibile stabilire il valore del potenziale elettrico, con la convenzione che a terra questo sia nullo. Se aggiungiamo una costante arbitraria al potenziale elettrico, che diventa così traslato, la misura del campo elettrico non cambia: per questo motivo, quello che misuriamo concretamente con il voltmetro è una differenza di potenziale. E quando andiamo a studiare le equazioni di Maxwell per un sistema con potenziale traslato, vediamo che le soluzioni non cambiano e quindi che la fisica è la stessa. Si dice che il campo elettrico è invariante per trasformazioni di gauge. L’invarianza per simmetrie è legata a quantità conservate, in questo caso la carica elettrica. Cambiando il gruppo di simmetria, si possono ottenere altre teorie adatte a descrivere sistemi fisici diversi.

Il più grande successo delle teorie di gauge è il Modello Standard delle particelle elementari, in cui c’è un gruppo enorme di simmetrie che codificano tre delle quattro forze fondamentali (interazione forte, elettromagnetica e debole) e tutte le particelle collegate. Le sue predizioni sono state verificate sperimentalmente con un altro grado di precisione, come sappiamo dalle notizie recenti che ci arrivano dal CERN di Ginevra.

Quali sono le caratteristiche della geometria non commutativa?
La geometria non commutativa è stata sviluppata dal francese Alain Connes e usa i metodi che provengono dall’analisi funzionale e dall’algebra per studiare problemi geometrici. È una branca della matematica molto interessante, con varie applicazioni, dal modello standard delle particelle elementari (di cui si è occupato tra gli altri anche Walter van Suijlekom, con cui lavoro a Nijmegen) fino ai più recenti isolanti topologici (materiali che a volte si comportano da isolanti e a volte da conduttori).

In generale, la proprietà commutativa dice che se in un’operazione si scambiano due elementi, il risultato non cambia. Alcuni esempi classici sono la moltiplicazione e l’addizione, ma anche le traslazioni in uno spazio piatto: se ci spostiamo due metri verso nord e poi tre a est e ripetiamo i movimenti nell’ordine opposto, il punto di arrivo sarà lo stesso. Ci sono operazioni che non soddisfano la proprietà commutativa, per esempio la rotazione nello spazio di un oggetto: prendiamo un libro e facciamolo ruotare una volta di 90° lungo l’asse verticale e poi di altri 90° verso uno dei due assi orizzontali; ripetiamo l’operazione invertendo i passaggi e osserviamo la faccia del libro a cui ci ha portato la rotazione.

Il mio lavoro riguarda proprio operatori, cioè oggetti analitici di cui le rotazioni sono un caso particolare, dotati di un’operazione che non soddisfa la proprietà commutativa. La non commutatività è qualcosa di intrinsecamente presente nella formulazione matematica della meccanica quantistica, in cui le osservabili sono operatori, ed è il motivo per cui vale il principio di indeterminazione di Heisenberg. Non è possibile, infatti, misurare con precisione arbitraria due grandezze fisiche coniugate come la posizione e la velocità di una particella, perché se si misura prima la posizione e poi la velocità si ottiene un risultato diverso rispetto alla misura della velocità prima e della posizione poi.

La geometria non commutativa, inoltre, fornisce un linguaggio che permette di studiare oggetti, come gli spazi singolari, che i metodi classici della geometria algebrica e differenziale non riescono a descrivere.

Come si può applicare geometria non commutativa nello studio delle teorie di gauge?
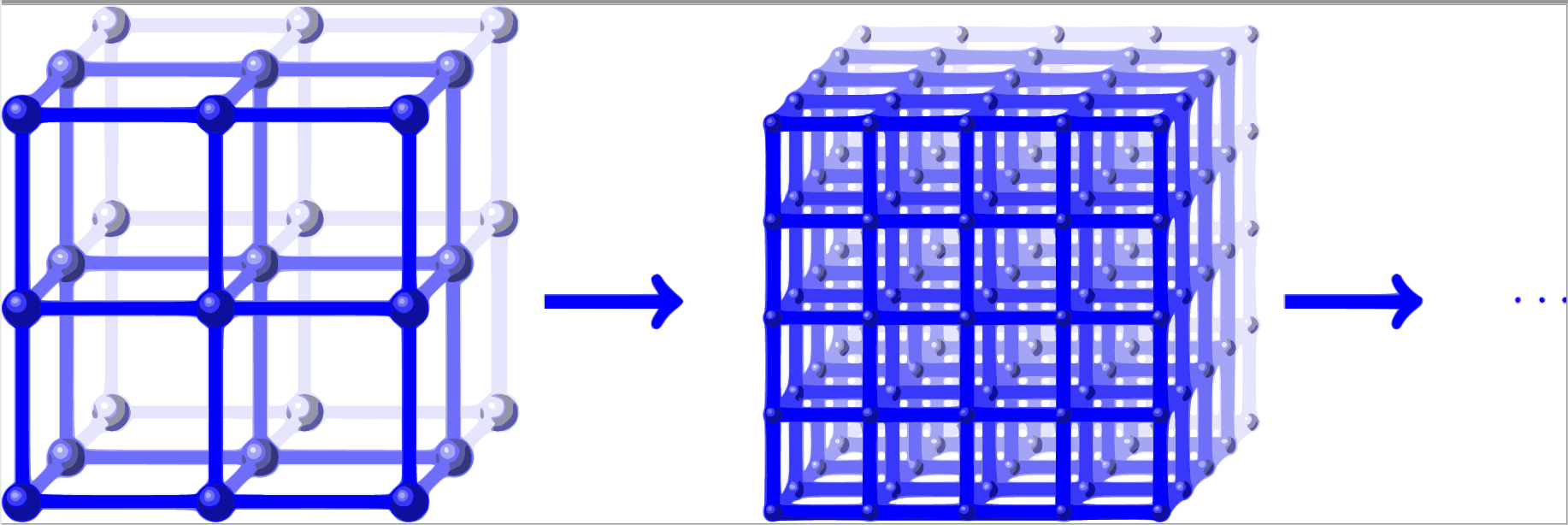
La quantizzazione delle teorie di gauge presenta svariate questioni aperte, tra cui una considerata tra i problemi del millennio. Nel mio gruppo di ricerca, ci occupiamo di un tipo particolare di teorie di gauge, quelle su reticolo. Il reticolo è una struttura geometrica invariante per traslazione, uno spazio finito facile da descrivere matematicamente. In questo spazio inseriamo delle particelle e cerchiamo di capire cosa succede quando queste sono soggette, per esempio, a un campo elettromagnetico. Ci proponiamo anche di studiare sistemi più complicati, come per esempio quello in cui la distanza tra i nodi del reticolo diventa sempre più piccola fino diventare uno spazio continuo, un po’ come quello in cui abbiamo l’impressione di vivere.

Per farlo, aumentiamo di volta in volta il numero di nodi e diminuiamo l’intervallo che li separa, creando un reticolo sempre più fine. A ogni passaggio definiamo un’algebra di operatori che dovrebbe rappresentare le osservabili del sistema quantizzato(come il momento e la posizione delle particelle), e una Hamiltoniana, cioè un operatore che ne descrive la dinamica. Anche questi oggetti varieranno di volta in volta e vogliamo riuscire a definire come le nuove osservabili e la nuova Hamiltoniana dipendono dal passaggio precedente in modo da ottenere informazioni sul limite nel continuo.

Quali sono le prospettive future del tuo lavoro?
La geometria non commutativa e in generale l’algebra degli operatori si sono rivelate un buon linguaggio per studiare la matematica della meccanica quantistica, della fisica delle particelle elementari, della teoria di gauge e adesso anche della materia condensata. Il mio obiettivo è continuare a studiare questo linguaggio, anche da un punto di vista puramente matematico, per cercare di renderlo il più chiaro possibile e vedere che aiuto può dare la matematica ad alcuni problemi fisici.

Leggi anche: L’indecidibilità approda nella fisica quantistica

Pubblicato con licenza Creative Commons Attribuzione-Non opere derivate 2.5 Italia.