Elettronica, nuovi materiali e carta da parati

TECNOLOGIA – Cosa c’entrano le caratteristiche della carta da parati con lo sviluppo dell’elettronica e cosa hanno a che fare con una forma esotica di materiali isolanti appena scoperta? Lo spiega un team di ricercatori in uno studio pubblicato su Science. La ricerca, frutto della collaborazione di gruppi di ricerca della Princeton University, della University of Pennsylvania, della Sungkyunkwan University, della Freie Universität Berlin e del Max Planck Institute of Microstructure Physics, è ricorsa proprio alle particolari proprietà matematiche che descrivono la struttura della carta da parati per analizzare le caratteristiche dei composti chimici. Questo ha permesso di individuare una nuova forma di materiali isolanti dotati di una superficie metallica e capace di condurre con proprietà molto promettenti per lo sviluppo dell’elettronica e forse anche del  calcolo quantistico.

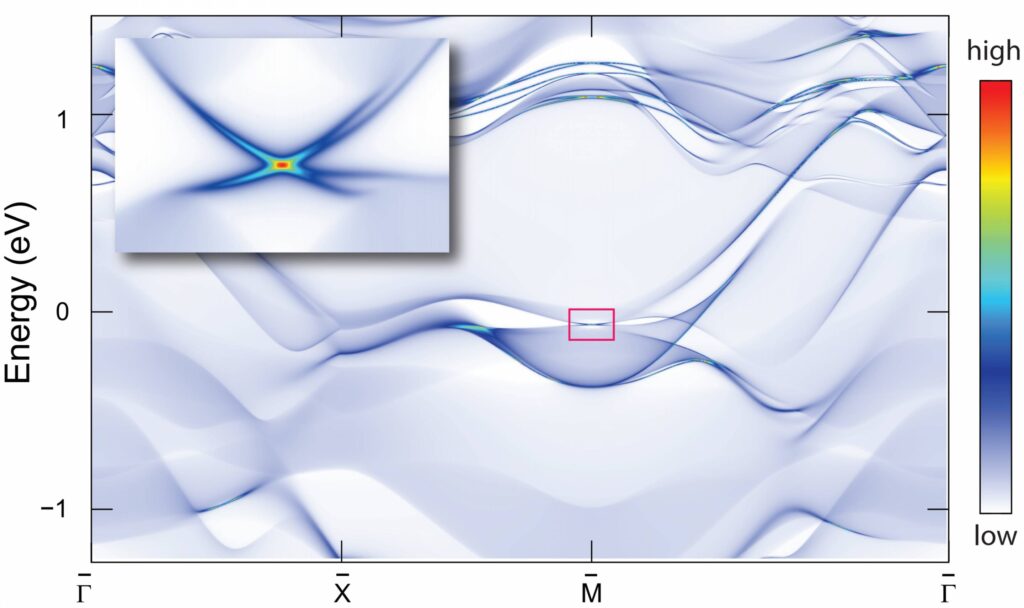
“La bellezza della topologia sta nel fatto che si possono applicare i principi della simmetria per trovare e categorizzare i materiali” racconta Andrei Bernevig, professore di fisica della Princeton, commentando le potenzialità di questa branca della matematica nello studio della struttura dei materiali.

Il risultato concreto dello studio è stata una lega di Piombo e Stronzio (Sr2Pb3), un materiale con una struttura tridimensionale che ha la caratteristica di combinare le particolari proprietà elettroniche del  grafene, che è bidimensionale, con quelle di materiali tridimensionali come gli isolanti topologici. Quest’ultimo è un particolare stato di aggregazione della materia scoperto in maniera indipendente nel 2005 da Charles Kane della University of Pennsylvania e dallo stesso Bernevig, autori anche della attuale ricerca, che dà origine a un materiale isolante all’interno, ma conduttore sulla superficie.

Isolanti topologici

“Puoi pensare gli isolanti topologici come degli Hershey’s kiss [cioccolatini molto noti negli USA, NdA],” ha affermato Kane, anche egli tra gli autori autori della ricerca. “Il cioccolato è l’isolante e la carta è il conduttore. Noi abbiamo provato a identificare nuove classi di materiali nei quali le simmetrie dei cristalli proteggono la superficie conduttiva. Quello che abbiamo fatto qui è identificare il tipo di isolante cristallino topologico più semplice”.

L’importanza di questo studio sta nel fatto che gli isolanti topologici potrebbero rivelarsi di grande importanza nello sviluppo di computer quantistici e proprio per questo dopo la loro scoperta si è cercato di combinare le loro proprietà con quelle del grafene. Gli elettroni che conducono la corrente nel grafene possono assumere dei particolari gruppi di stati che formano i cosiddetti coni di Dirac. In particolare nel grafene ci sono 4 coni di Dirac legati due a due. L’esistenza di questi stati fa sì che la conduzione elettrica possa avvenire come se fosse dovuta ad elettroni privi di massa e capaci di spostarsi a velocità relativistiche. La superficie degli isolanti topologici ha una caratteristica simile, ma presenta solo un singolo gruppo di questi stati.

Potrebbe essere possibile allora che esistano isolanti topologici con caratteristiche simili al grafene e che abbiano due coni di Dirac legati? E’ proprio questo ciò che si è domandato Kane. In questo modo si combinerebbero le proprietà elettroniche dei due materiali, ma come racconta “quello che ho realizzato è che un singolo paio di coni di Dirac è impossibile in un materiale puramente bidimensionale, ma potrebbe essere possibile sulla superficie di un nuovo tipo di isolante topologico. Ma quando ho provato a costruire questo stato, i due coni uscivano slegati”.

La soluzione dell’enigma di Kane era a Princeton in un nuovo tipo di isolanti topologici appena scoperto. Quando Benjamin Wieder, allievo di Kane e ora postdoc a Princeton, visitò il suo futuro posto di lavoro, venne a conoscenza di questi  nuovi materiali e interpretò le loro caratteristiche come se fossero dei cristalli tridimensionali avvolti in un tipo speciale di carta da parati.

Ecco la chiave per ottenere un isolante di Dirac. Si tratta di trovare “un cristallo che sembri come se sia avvolto nella giusta carta da parati” spiega Weiner. Si tratta quindi di interpretare la superficie degli isolanti in termini di carta da parati, in modo da riconoscere quali delle sue caratteristiche di simmetria consentono di poter stabilizzare un coppia di coni di Dirac.

A questo punto i ricercatori si sono messi subito all’opera per formalizzare dal punto di vista matematico l’ispirazione di Weiner e il risultato è stato una nuova metodologia basata sulla simmetria della carta da parati per la diagnosi della topologia dei cristalli tridimensionali. “I pincipi base sono abbastanza semplici da averli schematizzati quello stesso pomeriggio”, “ma nonostante ciò sono abbastanza solidi da predire e comprendere uno zoo di nuove fasi topologiche nei materiali” sono stati i commenti rispettivamente dei ricercatori Bradlyn e Wang, entrambi tra gli autori dello studio. Questa intuizione ha così permesso agli scienziati per la prima volta di mettere direttamente in relazione la simmetria di una superficie con la presenza degli stati topologici di superficie desiderati ottenendo così una tecnica elegante e di immediato utilizzo.

A questo punto però si trattava di metterla alla prova dal punto di vista pratico e trovare effettivamente un materiale che combinasse le proprietà degli isolanti topologici e del grafene. Per identificarlo i ricercatori hanno analizzato centinaia di sostanze attraverso la nuova tecnica trovando alla fine la risposta nel piombo-stronzio.

Dato che vengono di continuo scoperti isolanti topologici ancora più esotici, si tratta di una scoperta importante in quanto questo studio consente di porre su basi teoriche più solide il ruolo della simmetria wallpaper (dal nome in inglese della carta da parati) e degli speciali isolanti di Dirac.

Segui Vincenzo Senzatela su Twitter

Leggi anche: 4i, la tecnica innovativa per la medicina di precisione

Pubblicato con licenza Creative Commons Attribuzione-Non opere derivate 2.5 Italia.